This is the second post in a three-part series exploring the client-side GeometryEngine in the ArcGIS API for JavaScript. This series covers the following topics:
- Part 1: Testing spatial relationships and editing
- Part 2: Measurement
- Part 3: Overlay Analysis
Last week I gave an overview of GeometryEngine in the ArcGIS API for JavaScript and shared a sample that showcases its ability to enhance the user experience of editing geometries in web applications. I also shared a second sample to demonstrate its advantage over GeometryService in performance and speed.
Most of GeometryEngine’s methods can be categorized into one of three groups: testing spatial relationships, measurement, and overlay analysis.
In this post, we’ll take a look at some of the methods GeometryEngine exposes that allow one to measure lengths, areas, and distances. The editing sample mentioned in the first post uses geodesicArea to perform area calculations. Other measurement methods include distance, planarLength, geodesicLength, planarArea, buffer, and geodesicBuffer.
After glancing through this list, one of the first questions that come to mind is Why are there geodesic and planar versions of the same method?
In short, the geodesic method approaches measurement differently from the planar method and thus may generate different results depending on the geometry and the location. To illustrate this, I used the 4.0 beta 1 version of the ArcGIS JavaScript API to create the following sample comparing planar and geodesic buffers.
View Sample: Geodesic vs. Planar buffers
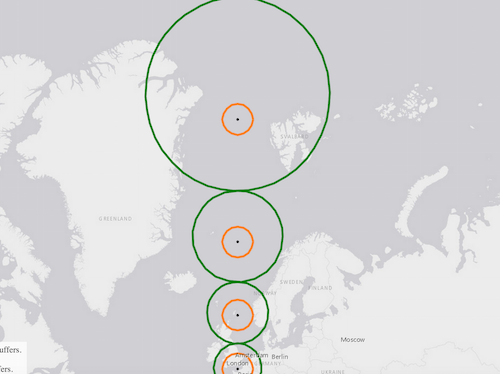
Notice how the shapes of the geodesic buffers (symbolized in green) become more distorted as they approach the poles, while the shapes of the planar buffers (symbolized in orange) are all equal. The only location where both geodesic and planar buffers are exactly the same size and shape is the equator.
So what’s going on here? It all relates to the shape of the earth and how we attempt to represent it with various types of projections.
Paying the price: distortion in map projections
First of all, we need to remember the earth is a geoid (spherical in nature) and maps often represent the earth on flat two-dimensional (or planar) surfaces. Projecting features and boundaries on the earth to a planar surface makes calculations such as area and length easier to perform. Planar measurement uses Cartesian coordinates to measure Euclidean distances on the projected plane. However, projections pay the price of one or more distortions to area, distance (length), shape, or direction.
Since the equator is the only place where Web Mercator minimizes distortion to shape and size, the planar buffer is only accurate on the equator. As planar buffers are drawn away from the equator, they preserve their shape; but doing so severely distorts their true location and area when drawn near the poles.
Geodesic tools: why and when to use them
Unlike planar measurements, geodesic methods use an algorithm that takes into account the curvature of the earth. The calculations are more complex, but the results are more accurate throughout the globe. Therefore, the geodesic buffers are actually more correct than planar buffers despite their lopsided shape near the poles. The following sample illustrates this same principle while measuring lines drawn on the map.
View sample: geodesic and planar length in Web Mercator
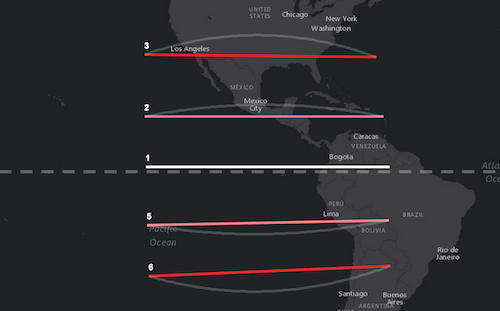
Open the sample and draw a line near the equator (the dashed white line). Draw additional lines north and south of the equator at various scales. Notice the differing results between the geodesicLength and planarLength methods for the same line. It’s pretty significant the farther lines are drawn away from the equator. A white transparent arc also draws alongside longer lines drawn north and south of the equator. This represents the great circle (or geodesic line) between the two end points of the line and represents the shortest path between the two points.
When possible, geodesic methods should be used in favor of planar methods because of their ability to minimize distortion regardless of the location of the input geometry.
Planar tools: why and when to use them
If geodesic methods are so much better at measurement, why provide planar methods at all? In the case of GeometryEngine, the geodesic tools only support two spatial references – WGS84 (wkid 4326) and Web Mercator (wkid 3857). Planar methods on the other hand, only accept geometries with projected coordinate systems (PCS). Since Web Mercator is a PCS, it may be used in planar measurements, but this isn’t recommended as evidenced by the samples above.
The following is the general rule to follow when measuring with GeometryEngine: use geodesic methods when working in WGS84 or Web Mercator and use planar methods when working with data defined in a PCS. Some localized coordinate systems, such as UTM and State Plane, are effective at minimizing all four distortion types. So as long as the data are located within the bounds of a single projection (and zone if applicable), planar calculations should yield results pretty close to reality.
This rule also implies that one uses the proper projection for their data prior to using planar measurement methods. Failure to respect the bounds or limitations of map projections will likely yield inaccurate results. The spatial reference of the map in the following sample, for example, is in the Illinois East zone of the State Plane PCS. Once the map loads, the user can create geometries (in this case, lines) anywhere on the map.
View sample: Planar measurement in a PCS
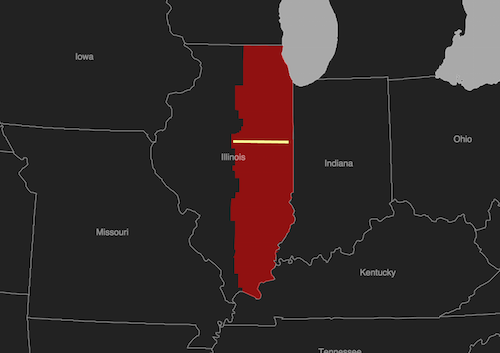
The area shaded in red depicts the Illinois East zone of the State Plane coordinate system. As long as geometries are created within these bounds, the planar length will be accurate and equal to geodesic measurements made using GeometryService. Creating geometries outside the zone, however, will produce measurements that are inaccurate. If one needs to create and measure geometries that span different zones, a different projection should be used such as Web Mercator, which allows for measuring geometries anywhere using a geodesic algorithm.
Other coordinate systems
While GeometryEngine provides methods for quick and easy calculations of length, area, and buffers client-side, there are spatial references that GeometryEngine does not support. These include all geographic coordinate systems (GCS) other than WGS84. When measurements or buffers need to be created using data in any GCS other than WGS84, GeometryService should be used.
GeometryService also is the best alternative when working with data defined in a PCS that doesn’t play well with Euclidean measurements, such as the spatial reference in the following sample.
View sample: planar length in Goode’s Homosoline
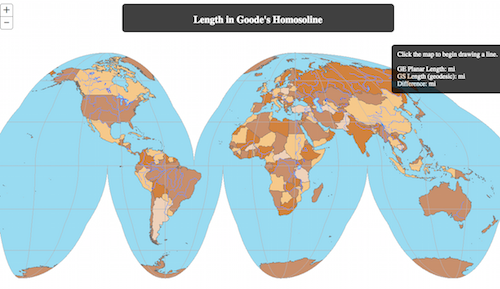
Similar to Web Mercator, the Goode’s Homosoline projection only allows for accurate length measurements on the equator. Since GeometryEngine’s geodesicLength method doesn’t support this spatial reference, GeometryService is the only alternative for providing accurate length measurements throughout the projection.
In these cases, if measurement plays a critical part in the application, the data should either be defined in a PCS more suited for measurement, or GeometryService should be used. Accurate measurement is a necessity in any GIS. Because it handles all computation client-side, GeometryEngine makes measuring and buffering fast and simple.
Keep an eye out next week for the final part of the GeometryEngine series when we take a look at some of its analysis and overlay methods.

Article Discussion: