By Aileen Buckley, Mapping Center Lead
The vertical change in the elevation of the land surface, when determined over a given horizontal distance-along a road or stream, for instance-is known as its slope (figure 1). There are three primary ways to quantitatively express the slope between two points. In each, the lower the slope value, the flatter the terrain, and the higher the slope value, the steeper the terrain. The slope values may be expressed as a ratio, as a percentage or as an angle.
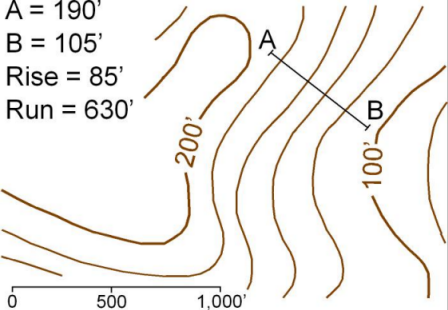
Figure 1. Slope is computed from the elevation difference (rise) between two points A and B on a topographic map and the horizontal distance (run) between the two points.
Slope Ratio
The simplest way to express slope is to describe the slope as the slope ratio between the elevation difference (rise), and the ground distance (run) between the two points (figure 2). Mathematically, this is written as y/x. In figure 1, a rise of 85 feet over a run of 630 feet gives a slope ratio of 85/630, which is 0.13. Slope ratios can also be negative-a fall of 30 feet over a run of 150 feet gives a slope ratio of -30/150, which is -0.20. Notice that the vertical and horizontal distances must always be in the same units of measurement.
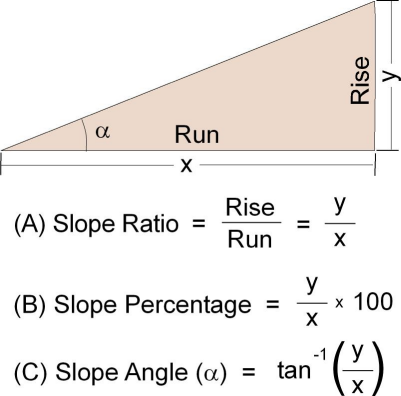
Figure 2. The slope of a surface between two points can be expressed as a ratio (A), as a percentage (B), or as an angle (C), where tan-1 is read as “angle whose tangent is…”
Slope Percentage
You can also express the ratio as a slope percentage (also called percent rise) (figure 3). To do so, simply multiply the slope ratio by 100. In the example above, the slope ratio 0.13 is also 0.13 * 100, or 13%. Slope percentages range from 0 to near infinity. A flat surface is 0 percent, and as the surface becomes more vertical, the slope percent becomes increasingly larger. In figure 2, you can see that when the angle is 45 degrees, as in triangle B, the rise is equal to the run, and the slope percent is 100 percent. As the slope angle approaches vertical (90 degrees), as in triangle C, the slope percent approaches infinity.
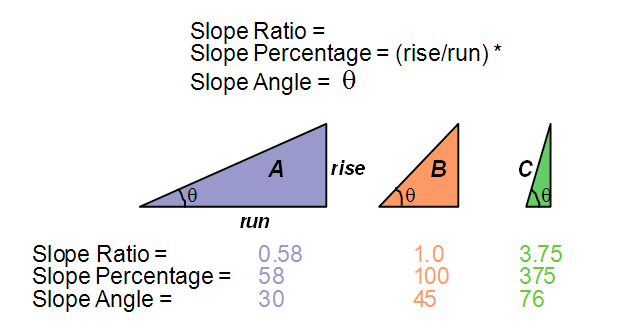
Figure 3. These triangles help demonstrate the comparison of the values for expressing slope as a ratio, as a percentage and in degrees.
Slope Angle
A third way to express slope is in degrees that relate to the slope angle (figure 3). Slope angle values range in degrees from 0 to 90. This way of specifying slope is based on the fact that the slope ratio (y/x) is the trigonometric tangent of the slope angle. Consequently, the slope angle is the inverse tangent (tan-1) of the slope ratio (the angle whose tangent is the slope ratio). A slope angle of 45° is a 100% slope, since this is the angle whose tangent and slope ratio is 1.0.

Commenting is not enabled for this article.