Using imputation intelligently
Missing data occurs in many spatial datasets. Data might be missing because a sensor is temporarily broken, a sampling site is inaccessible, or data values are intentionally suppressed to protect confidentiality.
If any variable for an observation is missing, a common way to deal with this situation is to delete that observation from the dataset. However, rather than throwing out valuable data that can impact analyses or result in “holes” in the map, missing data values can be “filled in” using other information from the dataset. In the case of spatial data, the values of neighboring features in space can be used to create an estimate for missing values. For spatiotemporal data, neighbors in time can be used to fill in the missing values.
We can feel confident doing this, in part, because of Waldo Tobler’s first law of geography. It states that “everything is related to everything else, but near things are more related than distant things.” [Tobler is an American geographer who was a pioneer in the development of analytical cartography and computational geography and a leading contributor in the field of quantitative spatial analysis.]
Tobler’s law implies that the values of the missing data will be like the values of its neighbors in space and/or time. Therefore, we can use average, minimum, maximum, or median of the neighboring values to fill in the missing value. Statisticians call filling in missing values imputation or, in the case of spatial data, geoimputation.
While filling in missing values may seem harmless on the surface, it can potentially produce problematic or unwanted consequences. Statistical analyses with data that has been filled in can produce biased and misleading results. In statistical terms, imputation leads to narrower confidence intervals, underestimation of standard errors and, thus, overestimation of test statistics. Nonetheless, it is often necessary to fill in missing values so that we can produce an aesthetically pleasing map or perform a spatial analysis on the entire study area, but filling in missing values should be done with caution using best practices for imputation.
Some Cautionary Notes
Before you start filling in values, make sure you understand your data and determine which values are missing. The placeholder indicating a missing data value can vary from dataset to dataset. In a geodatabase feature class, missing values are stored as null values, written as <Null>, and thus clearly recognizable.
However, shapefiles cannot store null values. Tools or other procedures that create shapefiles may store or interpret a null value as zero. In some cases, null values in a shapefile are indicated by a very large positive or negative number.
A simple trick for discovering missing data values is sorting the field of interest from largest to smallest values and then from smallest to largest values. This will let you more easily see null values, zero values, or extremely large or small values. This may provide clues for identifying the placeholder used to indicate a missing value. Metadata sometimes indicates the placeholder for missing data.
Next, determine how many values are missing since you don’t want to fill too many values. While there is no absolute cutoff for the number of missing data values you should attempt to fill in, a common rule of thumb is to fill in no more than 5 percent of the values in a dataset.
Finally, determine where the missing values are located. Map the attribute with missing data and explore its spatial patterns. Determine if missing data values are clustered or located on the periphery or in the core of your study area. See if the missing values appear to be in areas of primarily high or low values. Any of these situations suggest that there is a pattern to the location or values of missing data. Patterns can indicate that data is not missing at random. Filling in missing values works best when missing data is missing at random.
How Will You Fill in Missing Values?
When filling in missing values, you must decide on a fill method. Should you use the minimum, maximum, median, or average of neighboring values?
If you want to underestimate filled-in values, use the minimum of neighboring values. For example, you might want to underestimate if you are trying to fill in missing data on the number of students who receive free lunches.
If you don’t want to underestimate the missing values, use the maximum. For example, if you were filling in values in a dataset describing the number of people who have higher educational degrees.
If you suspect the presence of outlier high or low values locally, use the median. This might be most appropriate for data that often contains outliers.
If Tobler’s first law seems to apply to the dataset, missing values will tend to be like neighbor values, so use the average.
You also must decide how to define the set of neighbors that will be used to calculate missing values. Neighbors can be defined based on a variety of spatial relationships. You can define a fixed number of neighbors, choose all neighbors within a fixed distance, or choose neighbors that are contiguous (i.e., share a border or have corners that touch).
Which fill method and which neighbors you use depend on how the filled data will ultimately be used. For example, a cartographer may want to fill polygons containing missing data to create an aesthetically pleasing map without holes. In this case, calculating the average of many spatial neighbors would be effective. A soil scientist who is filling in a missing soil moisture measurement resulting from a broken sensor will use neighbors within a fixed distance and calculate their median to avoid the influence of outliers.
When deciding how to define the neighborhood and choosing fill method, think carefully about which of the surrounding features legitimately influence the features with missing values. Choose the fill method that is least likely to bias the results of analysis.
For example, a local public health analyst, who has childhood lead poisoning data at the census block group level, is missing data for a few block groups. That analyst might consider using the maximum values from neighboring block groups that share a border with the block group missing data to fill in the missing data. Using contiguous block groups can be justified because these locations will likely contain houses similar in age. Owing to changes in building practices over time, the age of houses is a known risk factor for lead exposure. While using the maximum value of the surrounding block groups to fill missing values might overestimate the true level of lead poisoning, when estimating risks to children’s health, it is better to overestimate—rather than underestimate—the potential for lead poisoning.
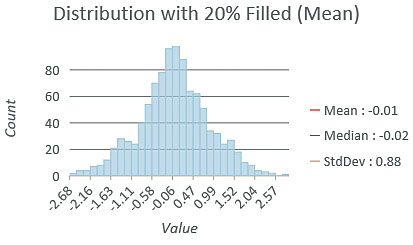
Understanding the Impacts of Filling in Missing Values
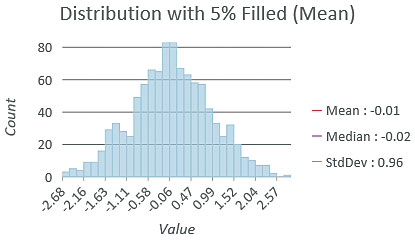
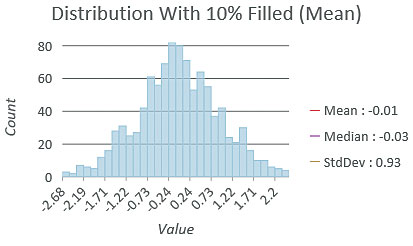
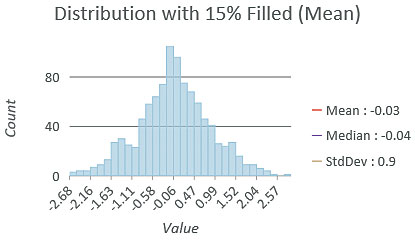
All fill methods will likely change the distribution of the data. This is important when making statistical assumptions about data or mapping it. When using graduated colors in a choropleth map, a map of the original data may be different from a map that includes filled values because class breaks can change if the distribution changes. A bell-shaped (normal) distribution is required for some statistical tests. If the data will be used in a statistical analysis, filling missing values could result in a distribution that is skewed or has less variability. A best practice is to map and explore the distribution of the data before and after filling in missing values.
If the data has a bell-shaped distribution, filling in values with the average of neighbors will tend to increase the number of values around the mean and pull in the tails of the distribution, thus decreasing the variability in the data (that is, reducing the standard deviation). Filling in the values with the minimum value can produce a negative-skewed distribution (more low values), and filling in with the maximum can produce a positive-skewed distribution (more high values).
The impacts of filling in missing values on statistical analyses are more difficult to determine, particularly if the analyses involve calculating local statistics. For example, hot spot analysis (Getis-Ord GI*) compares a local statistic to the global average. Filling in missing values can skew the distribution so that the mean of the dataset will be different once missing values are filled in. Since the impact of filling in missing values is difficult to predict, a best practice is to perform the statistical analysis before and after filling in missing values to compare the results.
Filling in Missing Values with ArcGIS Pro
With the release of ArcGIS Pro 2.0, the Space Time Pattern Mining toolbox contains a new tool for filling in missing values. The Fill Missing Values tool supports filling in missing values with the minimum, median, maximum, or average of neighbors. It also allows you to define the neighbors in a variety of ways: set number of nearest neighbors, neighbors within a fixed distance, contiguous neighbors, or neighbors defined by an input file.
Additionally, the neighbors can be in both space and time. The temporal trend option fills in missing values using the time series at each location. Three types of input data are supported: a feature class with no associated temporal data, a feature class in which each feature is repeated for every time step, and a feature class with temporal data stored in a related table. The Fill Missing Values tool provides information about the distribution of the data before and after filling missing values as well as the total number and percentage of values filled. For help getting started with Fill Missing Values, see the ArcGIS Pro online help.
More Best Practices for Filling in Missing Values
There are several additional best practices to follow when filling in missing values. Check the number and percentage of values filled in to determine if any values are still missing. If they are, try changing the method used to fill the values. This might mean increasing the number of neighbors or size of the neighborhood. Be sure not to fill in missing values with values you already filled in. This is bad practice because you are essentially estimating values from estimates.
Examine the distribution of the data before and after filling in missing values by comparing descriptive statistics such as the mean and standard deviation and examining a histogram of the data to check for skewing, elevating, or flattening of the curve. An ideal solution would yield distributions that are similar in shape.
Look for local or regional applicability of the method used to fill in values. The method used to fill in values may have worked better in some areas than in others. For example, if you are filling using the average of neighboring values and the range of the reported standard deviations is wide, you might try varying the method by using a different type of neighborhood or a different fill method. Ideally, the standard deviation would be about the same for all filled values, indicating that they all vary similarly from the neighbors used to fill in the values.
-
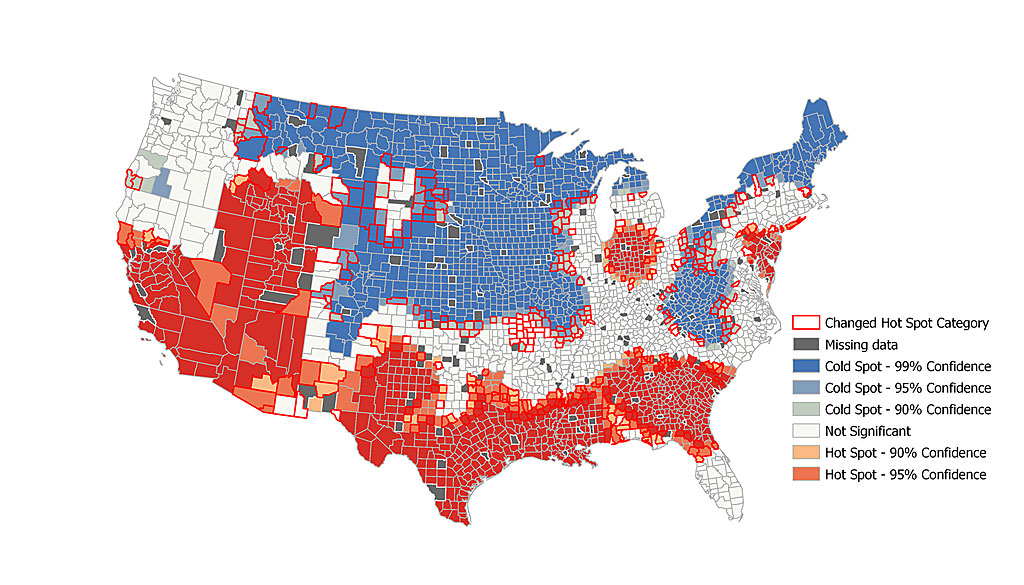
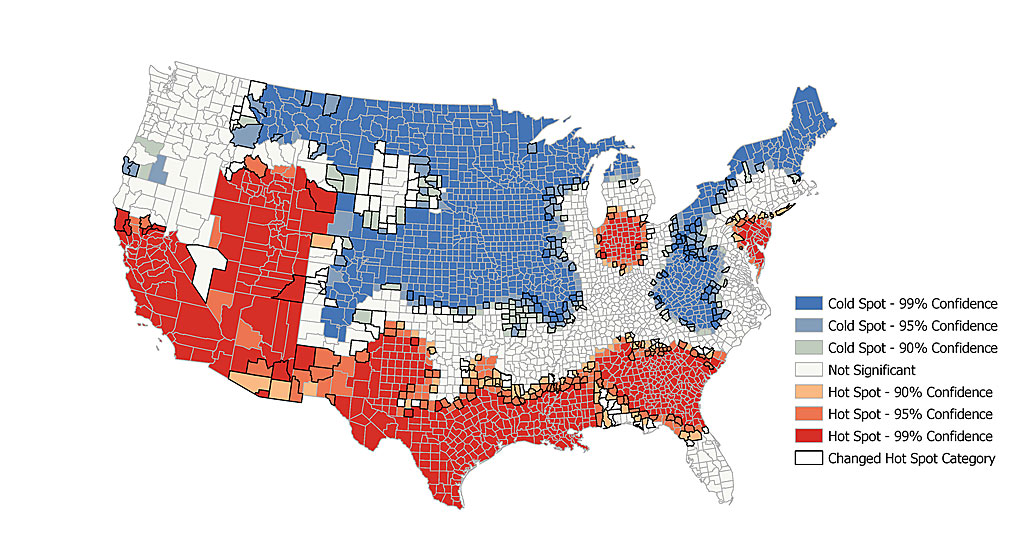
Both maps show hot spot analysis of 2010 average household size by US county, however the second map has 5% of the missing data filled in. Counties with a bold outline indicate a change in hot spot category after filling in the missing values. While the overall spatial pattern did not change, many counties on the peripheries of hot and cold spots changed category.
Think about how the data will be used once the values have been filled in. If the data will simply be mapped to create an aesthetically pleasing visualization without holes, minor variations in the filled values may be masked by the mapping method. Choropleth mapping typically classifies data into several classes, so variations within classes will not be apparent. On the other hand, if data will be used to generate official statistics, the impact of filling in missing values must be carefully examined and clearly understood.
Finally, communicate to your audience that you have filled in missing values. If you are writing a report, describe the method you used to fill the missing values and state any assumptions you made when choosing the method to fill in the values. If you are making a map, consider identifying the features for which the values have been filled in on a separate map. Cartographers have also identified polygonal features with filled in values using a hatched or stipple pattern or a unique feature outline. Be careful when using these methods as they can obscure the polygon fill or change the way the color of the fill is seen.
Following the guidelines described in this article thoughtfully when filling in missing values will help you avoid biased and misleading results in maps and analyses.
About the Authors
Kevin A. Butler is a product engineer on the Esri Spatial Statistics team and a member of Esri’s Virtual Science team. He holds a doctorate in geography from Kent State University.
Aileen Buckley is a research cartographer and a member of Esri’s virtual science team. She holds a doctorate in geography from Oregon State University.