You will usually georeference raster data using existing spatial data (target data), such as georeferenced rasters or a vector feature class that resides in the desired map coordinate system. The process involves identifying a series of ground control points—known as x,y coordinates—that link locations on the raster dataset with locations in the spatially referenced data.
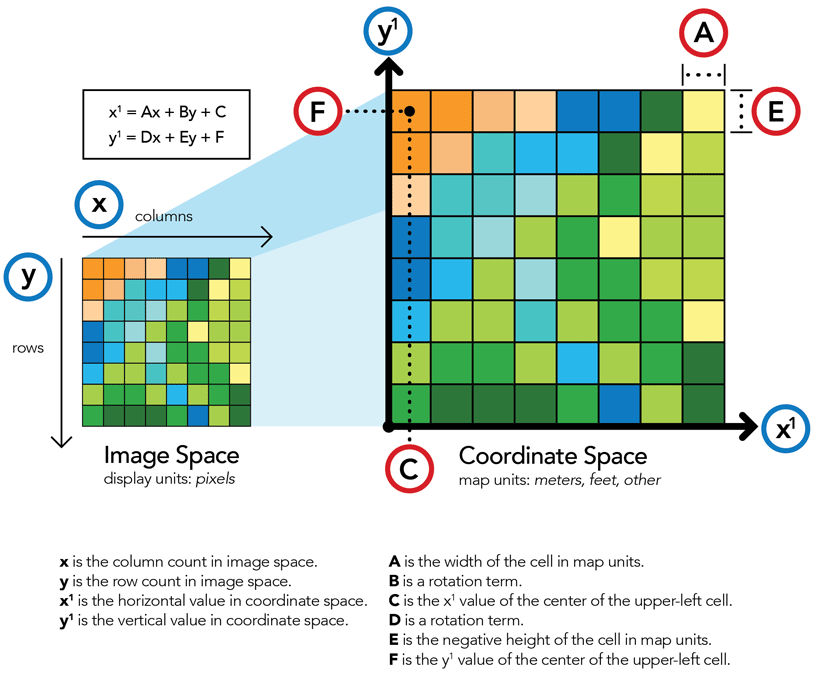

Control points are locations that can be accurately identified on the raster dataset and in real-world coordinates. Many different types of features can be used as identifiable locations such as road or stream intersections, the mouth of a stream, or corner of an established field. The control points are used in conjunction with the transformation to shift and warp the raster dataset from its existing location to the spatially correct location. The connection between one control point on the raster dataset (the from point) and the corresponding control point on the aligned target data (the to point) is a control point pair.
The number of links you need to create depends on the complexity of the transformation you plan to use to transform the raster dataset to map coordinates. However, adding more links will not necessarily yield a better registration. If possible, you should spread the links over the entire raster dataset rather than concentrate them in one area. Typically, having at least one link near each corner of the raster dataset and a few throughout the interior produces the best results.
Generally, the greater the overlap between the raster dataset and target data, the better the resulting alignment, because you’ll have more widely spaced points with which to georeference the raster dataset. For example, if your target data only occupies one-quarter of the area of your raster dataset, the points you could use to align the raster dataset would be confined to that area of overlap. Thus, the areas outside the overlapped area are not likely to be properly aligned. Keep in mind that your georeferenced data is only as accurate as the data to which it is aligned. To minimize errors, you should georeference to data that is at the highest resolution and largest scale that is appropriate for your application needs.
When you’ve created enough control points, you can transform the raster dataset to the map coordinates of the target data. Depending on the number of control points, you can use one of several types of transformations available in ArcGIS Pro to determine the correct map coordinate location for each cell in the raster.
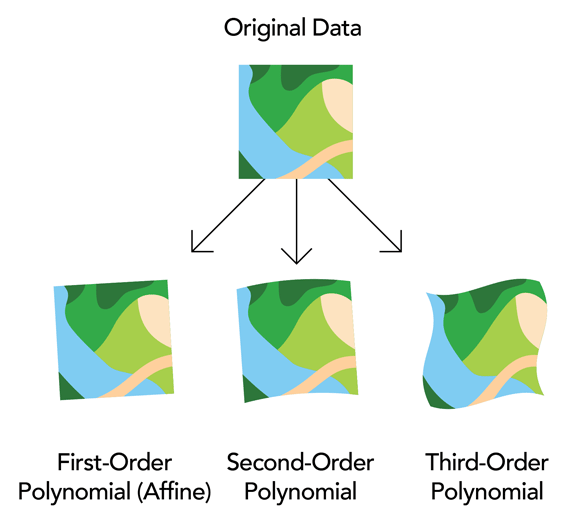
Polynomial transformations use a polynomial built on control points and a least-squares fitting (LSF) algorithm. These transformations are optimized for global accuracy but do not guarantee local accuracy. Polynomial transformations yield two formulas: one for computing the output x-coordinate for an input (x,y) location and one for computing the y-coordinate for an input (x,y) location. The goal of the LSF algorithm is to derive a general formula that can be applied to all points, usually at the expense of slight movement of the two positions of the control points. The number of the noncorrelated control points required for this method must be one for a zero-order shift, three for a first-order, six for a second order, and ten for a third order. The lower-order polynomials tend to give a random type error, while higher-order polynomials tend to give an extrapolation error.
A zero-order polynomial is used to shift your data. This is commonly used when your data is already georeferenced, but a small shift will better line up your data. Only one control point is required to perform a zero-order polynomial shift. It may be a good idea to create a few control points, then choose the one that looks the most accurate.
The first-order polynomial transformation is commonly used to georeference an image. Use a first-order, or affine, transformation to shift, scale, and rotate a raster dataset. This generally results in straight lines on the raster dataset mapped as straight lines in the warped raster dataset. Thus, squares and rectangles on the raster dataset are commonly changed into parallelograms of arbitrary scaling and angle orientation.
With a minimum of three control points, the mathematical equation used with a first-order transformation can exactly map each raster point to the target location. Any more than three control points introduces errors (or residuals) that are distributed throughout all the control points. However, you should add more than three control points, because if one control is inaccurate, it has a much greater impact on the transformation. Thus, even though the mathematical transformation error may increase as you create more links, the overall accuracy of the transformation will increase.
The higher the transformation order, the more complex the distortion that can be corrected, but transformations higher than third order are rarely needed. Higher-order transformations require more links and will involve progressively more processing time. In general, if the raster needs to be stretched, scaled, and rotated, use a first-order transformation. If the raster dataset must be bent or curved, use a second- or third-order transformation.


