ArcUser Online
Finding a Meaningful Model
This checklist will help you evaluate regression models
By Lauren Rosenshein, Lauren Scott, and Monica Pratt, Esri
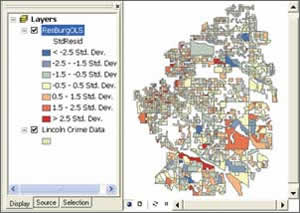
Figure 1: Mapping regression residuals from the model. Analyzing the residuals is an important step in finding a good model.
This article as a PDF.
The spatial statistics tools in ArcGIS let you address why questions using regression analysis. Regression models help answer questions like
- Why are there places in the United States with test scores consistently above the national average?
- Why are there areas of the city with such high rates of residential burglary?
Regression analysis is used to understand, model, predict, and/or explain complex phenomena. Because the spatial statistics tools used for regression analysis are part of the ArcGIS geoprocessing framework, they are well documented and accessed in a standard fashion.
However, coming up with a properly specified regression model to answer a specific why question can be challenging. What is a properly specified model? It is a model we can trust—one that is unbiased (i.e., predicts well in all parts of the study area) and includes all the key variables that explain the phenomenon you are examining. This article will step you through a process for evaluating regression models using a list of six checks and the Ordinary Least Squares (OLS) and Geographically Weighted Regression (GWR) tools in the ArcGIS Spatial Statistics toolbox.
Applying Regression Analysis
Regression analysis is all about explaining a phenomenon, such as childhood obesity, using a set of related variables, such as income, education, or access to healthy food. Typically, regression analysis helps answer why questions so you can do something about them. For example, by using regression analysis, you might discover that childhood obesity is lower in schools that serve fresh fruits and vegetables at lunch. That information can influence decisions about school lunch programs. Likewise, knowing the variables that explain high crime rates can help you make predictions about future crime so that prevention resources can be allocated more effectively. [For more information on regression analysis, see "Answering Why Questions: An introduction to using regression analysis with spatial data" in the Spring 2009 issue of ArcUser.]
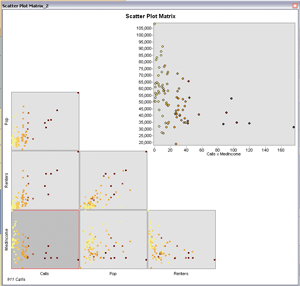
Figure 3: The scatterplot matrix can be used to evaluate all the relationships between the variables in your data. It is a graphic that displays two types of numeric data for each variable to determine if there is a relationship between them.
Unfortunately, it isn't always easy to find a set of explanatory variables that will allow you to model your question or explain the phenomena you're interested in. However, OLS regression, the best-known regression technique, includes information that can tell you when you've found a good model. The documentation for this tool also includes a guide that alerts you to the six tests your model should pass before you can feel confident you have a properly specified model.
This article examines these six checks and the techniques you can use to solve some of the most common regression analysis problems. Finding a properly specified model is often an iterative process, and these resources will make your work easier.
Choosing Appropriate Variables
Choosing the variable that you want to understand, predict, or model is the first task. This variable is known as the dependent variable. Test scores, crime, and childhood obesity were the dependent variables being modeled in the examples previously described.
Figure 4: Check variables to see if you have represented them in a way that will truly reflect a linear relationship.
Next, decide which factors might help explain the dependent variable. These variables are known as the explanatory variables. In the childhood obesity example, the explanatory variables might be things such as income, education, or access to healthy food. Identifying all the explanatory variables that might be important will require research. You'll want to consult theory and existing literature and talk to experts. Always rely on your common sense. Conducting preliminary research increases your chances of finding a good model.
With the dependent variable and the candidate explanatory variables chosen, running your analysis is the next step. The regression tools in ArcGIS are found in the Spatial Statistics toolbox in the Modeling Spatial Relationships toolset. Always start with OLS regression, because it provides important diagnostic tests that let you know if you've found a good model or if you still have some work to do.
The OLS tool generates several outputs including a map of the regression residuals and a summary report. The regression residuals map shows the over- and underpredictions from your model. Analyzing it is an important step in finding a good model. The largely numeric OLS summary report includes diagnostics you will use when going through the six checks discussed throughout the rest of this article.
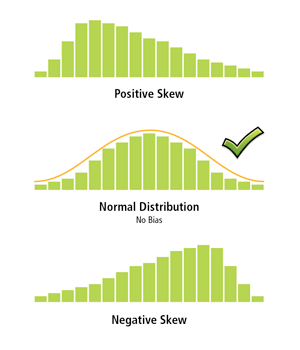
Figure 5: With a biased model, the distribution of the residuals is unbalanced, and results predicted by these models can't be trusted.
1: Are these explanatory variables helping my model?
After consulting theory and existing research, you will have identified a set of candidate explanatory variables. You'll have good reasons for including each one in your model. However, after running your model, some explanatory variables will be statistically significant, and some will not.
How will you know which are significant? The OLS tool calculates a coefficient for each explanatory variable in the model and performs a statistical test to determine whether that variable is helping your model explain the phenomenon. The statistical test computes the probability that the coefficient is actually zero. If a coefficient is zero (or very near zero), the associated explanatory variable has very little impact on your model. In other words, that variable is not helping.
The smaller the probability is, the smaller the likelihood that the coefficient is zero. When the probability is smaller than 0.05, an asterisk next to the probability on the OLS summary report indicates that the associated explanatory variable is helping your model (i.e., its coefficient is statistically significant at the 95 percent confidence level). So when looking for explanatory variables associated with statistically significant probabilities, look for ones with asterisks.
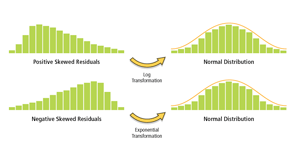
Figure 6: Histograms created for each explanatory variable can show if they are strongly skewed. This type of model bias may be removed by applying log or exponential transformations that place data in it.
The OLS tool computes both the probability and the robust probability for each explanatory variable. (Robust probabilities are accurate even when the relationships being modeled aren't stationary.) With spatial data, it is not unusual for the relationships you are modeling to vary across the study area. These relationships are characterized as nonstationary. When the relationships are nonstationary, you can only trust robust probabilities to tell you if an explanatory variable is statistically significant or not.
How will you know if the relationships in your model are nonstationary? The Koenker test for nonstationarity is another diagnostic reported by OLS. The Koenker p-value reflects how likely it is that the relationships being modeled are consistent across the entire study area. If the Koenker p-value is small and statistically significant (as indicated by an asterisk), the relationships do vary across the study area and are therefore nonstationary. Be sure to consult the robust probabilities.
While finding a model with explanatory variables that have statistically significant coefficients, you will likely try a variety of OLS regression models. These coefficients (and their statistical significance) can change radically depending on the combination of variables in your model. Typically, you will remove explanatory variables from your model if they are not statistically significant. However, if theory indicates that a variable is very important, or if a particular variable is the focus of your analysis, you might retain it even if it's not statistically significant.
2: Are the relationships what I expected?
It is important to not only determine whether an explanatory variable is actually helping your model but also think about its relationship to the dependent variable.
The coefficient associated with each explanatory variable is either a negative or positive number. Suppose you were modeling crime and one of your statistically significant explanatory variables is neighborhood income. If the coefficient associated with the income variable is negative, it means that crime goes up as neighborhood incomes go down (a negative relationship). If you were modeling childhood obesity and access to fast food was an explanatory variable with a statistically significant positive coefficient, this would indicate that childhood obesity increases when the number of fast food opportunities also increases (a positive relationship).
When you create a list of candidate explanatory variables, you should include the relationship (positive or negative) you expect for each variable. It would be difficult to trust a model that tells you the opposite of what theory and/or common sense dictate. For example, if a regression model for predicting forest fire frequency returned a positive coefficient for the precipitation variable, that would indicate forest fires increase in locations with lots of rain—not an outcome you would expect.
Unexpected coefficient signs usually indicate other problems with your model that will surface as you continue through the six checks. You can only trust the sign and strength of your explanatory variable coefficients if your model passes all these checks.
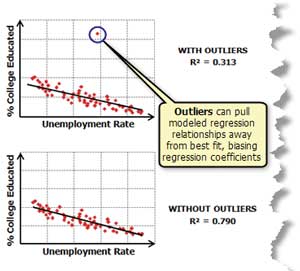
Figure 7: The presence of outliers can cause bias in a model. Use the scatterplot matrix to find these outliers and try running OLS both with and without the outliers to see how much impact they are having on model results.
3: Are there redundant explanatory variables?
When choosing explanatory variables, look for ones that address difference aspects of the phenomenon you are trying to model. Avoid redundant variables. For example, if you were trying to model home values, you probably wouldn't include explanatory variables for both home square footage and the number of bedrooms because both variables are related to home size. Including both could make your model unstable. Ultimately, you cannot trust your model if you have multiple variables that tell the same story.
How will you know if two or more variables are redundant? Fortunately, the OLS tool computes a variance inflation factor (VIF) value for each explanatory variable in your model. This value is a measure of variable redundancy that can help you decide which variables may be removed from your model without losing explanatory power. As a rule of thumb, a VIF value above 7.5 is considered problematic. If you have any variables with VIF values above 7.5, remove one variable at a time from the model and rerun OLS until you have removed the redundancy.
4: Is my model biased?
This may seem like a tricky question, but it is actually very simple to answer. When an OLS model is properly specified, the model residuals (i.e., the over -and underpredictions) have a normal distribution with a mean of zero (think bell curve). With a biased model, the distribution of the residuals is unbalanced. The impact of this bias may be that the model does well for low values but is ineffective for high values (or vice versa). For the childhood obesity example, this would mean that where you have low childhood obesity, the model is doing a great job, but in areas with high childhood obesity, predictions are off. Unfortunately, you cannot trust predictions from a biased model.
The good news is that there are a few strategies that often correct this problem. Sometimes the bias is the result of trying to model nonlinear relationships. In this case, creating a scatterplot matrix can be very useful. A scatterplot matrix is a graphic that displays two variables together. Linear relationships look like diagonal lines. Nonlinear relationships look more like curved lines. If your dependent variable has a nonlinear relationship with one of your explanatory variables, you have some work to do. OLS is a linear model that assumes that the relationships between your variables are linear.
If they aren't, you can try to transform your variables so that the relationships become linear. A histogram is another useful output from a scatterplot. Create one for each variable. If some explanatory variables are strongly skewed, you may be able to remove model bias by transforming them. Figure 6 shows how different types of transformations can help you get data into its most useful form. Model bias may also be a result of outliers influencing your model estimation. You can use the scatterplot matrix to find these too. Try running OLS both with and without the outliers to see how much impact they are having on your model results. If you find that the outliers represent bad data, you can remove them and continue your analysis without them.
5: Have I found all the key explanatory variables?
The standard output from OLS is a map of the regression residuals representing model over- and underpredictions. Red areas indicate that actual observed values are higher than values the model predicted. Blue areas show where actual values are lower than the model predicted. Statistically significant spatial autocorrelation in your model residuals indicates that you are missing one or more key explanatory variables.
How do you know if you have statistically significant spatial autocorrelation in your model residuals? For regression residuals, spatial autocorrelation usually takes the form of clustering: the overpredictions cluster together, and the underpredictions cluster together. You can run the Spatial Autocorrelation (Moran's I) tool from the Spatial Statistics toolbox on your regression residuals to see if the observed clustering is statistically significant or not. If the Spatial Autocorrelation tool returns a statistically significant z-score, it indicates that you are missing key explanatory variables.
Many analyses begin with a hypothesis that certain variables will be important. You might think 5 particular variables will be good predictors of the phenomenon you are trying to model. Or perhaps you think there could be 10 related variables. Although it is important to approach a regression analysis with a hypothesis, allow your creativity and insight to dig a little deeper and go beyond your initial variable list.
- Consider all variables that might impact the phenomenon you are trying to model.
- Review the relevant literature again.
- Create thematic maps for each candidate explanatory variable and compare those to a map of the dependent variable. Use your intuition to look for relationships in this mapped data.
- Try to come up with as many candidate spatial explanatory variables as you can (e.g., distance to urban center, proximity to major highways, or access to large bodies of water); these will often be critical to your analysis, especially when you believe geographic processes influence the relationships in your data. Until you find explanatory variables that effectively capture the spatial structure in your dependent variable, you will likely continue to have problems with spatial autocorrelation in your regression residuals.
- Examine the residual map and look for clues about what might be missing. If you notice, for example, that your model is consistently overpredicting in urban areas, perhaps you are missing some kind of urban density variable; if it looks like the overpredictions are associated with mountain peaks or valley bottoms, perhaps an elevation variable is needed. Do you see regional clusters of over- and underpredictions, or can you recognize a trend in the residual values? Sometimes creating dummy variables to capture regional differences or trends will resolve problems with statistically significant spatial autocorrelation. A classic example of a dummy spatial regime variable is one designed to capture urban/rural differences: assign all urban features a value of 0 and all rural features a value of 1. (Note: While spatial regime dummy variables are great to include in your OLS model, you will want to remove them when you run GWR; they aren't needed in GWR and will very likely create problems with local redundancy.)
You can also try running GWR and creating a coefficient surface for each candidate explanatory variable. Select one of your OLS models for this exercise. A good choice is a model with a high Adjusted R-Squared (R2) value that is passing all or most of the other diagnostic checks. Because GWR creates a regression equation for each feature in your study area, the GWR coefficient surfaces illustrate how relationships between the dependent variable and each explanatory variable fluctuate geographically. Sometimes you can see clues about potentially missing explanatory variables in these surfaces. You might notice, for example, that a particular explanatory variable is more effective near freeways but becomes less effective with distance from the coast or exhibits a strong east-to-west trend.
Finding those missing explanatory variables is often as much an art as a science. The process of finding them will often provide important insights into the phenomenon you are modeling.
6: How well am I explaining my dependent variable?
Now it's finally time to evaluate model performance. The R2 value is an important measure of how well your explanatory variables are modeling your dependent variable. Why leave this important check until the end? Because you cannot trust an R2 value unless your model has passed the other five checks. If your model is biased, it doesn't matter how high your R2 value is, because you can't trust your predictions. Likewise, if you have spatial autocorrelation of your residuals, you cannot trust the coefficient relationships or be sure your model will predict well for new observations. Once you have gone through the previous five checks and feel confident that you have met all the necessary criteria, it is time to figure out how well your model is explaining your dependent variable by assessing the R2 value. R2 values range between 0 and 1 and represent a percentage.
Suppose you are modeling crime rates and find a model that passes the first five checks with an R2 value of 0.65. This indicates that your explanatory variables tell 65 percent of the crime rate story, or to put it more technically, the model explains 65 percent of the variation in the crime rate variable. Is 65 percent good enough? Well, it depends. R2 values must be judged rather subjectively. In some areas of science, explaining 23 percent of a complex phenomenon is very exciting. In other fields, an R2 value may have to be closer to 80 or 90 percent to be considered notable. Either way, R2 values will help you judge the performance of your model.
Another important diagnostic for assessing model performance is known as Akaike's Information Criterion (AICc). The AICc value is a useful measure for comparing models that have the same dependent variables. You could use it to compare two models for student test scores when one model is based on socioeconomic variables and the other model is based on learning environments (e.g., classroom size, school facilities, tutoring programs). As long as the dependent variables for the two models are the same (in this case, student test scores), you can conclude that the model with the smaller AICc value performs better because it provides a better fit for the observed data.
What's Next?
Finding a properly specified OLS model (one that passes all six checks above) is definitely reason to celebrate. The next step is to try the variables from your OLS model in GWR. You should run GWR using the same dependent variable you used for OLS, along with the same OLS explanatory variables, with the exception of any spatial regime variables. Compare the GWR AICc value to the one you obtained from your properly specified OLS model. If the AICc value from GWR is smaller than the AICc value returned by OLS, you have improved your model (and your results) by allowing relationships to vary across your study area.
The GWR output feature class contains coefficients for every feature and every explanatory variable. Create maps of these coefficient values (standard deviation rendering is appropriate) to see where each explanatory variable is most important. Suppose one of your explanatory variables for a model of longevity is traffic accidents or crime. Determining where these variables are important predictors of longevity can help you decide where to implement policies to encourage longevity.
It is important that you find a properly specified OLS model before you move to GWR analysis. GWR will not identify missing explanatory variables or model bias problems and doesn't have diagnostic tools to help you correct these problems. The only reason you might move to GWR without a properly specified OLS model is if you are confident that the variation among the relationships you are modeling (i.e., its nonstationary nature) is the only reason you haven't found a properly specified model.
Evidence that nonstationarity is the culprit would be finding that the GWR coefficients for theory-supported explanatory variables change signs dramatically (i.e., in some parts of your study area, the coefficients are positive, and in other parts, they are negative). Similarly, if you find a properly specified OLS model for one portion of your study area, but a different model with different explanatory variables works for another portion of your study area, you have strong evidence that nonstationarity is making it difficult for your initial model to pass all the OLS checks. If you can determine that nonstationarity is the only issue with your OLS model, it is appropriate to move to GWR, because this method of regression analysis was specifically designed to capture and model spatial nonstationarity.
Don't Forget...
The most important thing to remember when you are stepping through the process of building a properly specified regression model is that the goal of your analysis is to understand your data and use that understanding to solve problems and answer questions.
You may try a number of models (with and without transformed variables), analyze your coefficient surfaces, and still not find a properly specified OLS model but—and this is important—you will still be contributing to the body of knowledge on the phenomenon you are modeling. Even if the model you thought would be a great predictor turns out to be insignificant, discovering that fact is incredibly helpful information. The process of trying to find a meaningful model is always a valuable exercise because you learn so much along the way. Applying this knowledge helps answer why questions so you can more effectively evaluate various courses of action and make better decisions.
For more information about regression and other tools in the Spatial Statistics toolbox, go to bit.ly/spatialstats.
About the Authors
Lauren Rosenshein works on the ArcGIS geoprocessing team and is responsible for software support, education, documentation, and development of spatial statistics tools. She received her master's degree in geographic and cartographic science from George Mason University and her bachelor's degree in geography from McGill University.
Lauren Scott has more than 20 years of experience in software development. She works on the ArcGIS geoprocessing team and is responsible for software support, education, documentation, and development of spatial statistics tools. She holds a PhD in geography from the joint doctoral program at San Diego State University in California and the University of California, Santa Barbara.
Monica Pratt is the founding and current editor of ArcUser magazine and Esri publications team lead. She has more than 100 published articles on GIS and related technology topics and is a contributor to Web GIS: Principles and Applications, published by Esri Press.
