ArcUser Online
| Understanding Topology by David M. Theobald, Colorado State University |  |
|
When asked if topology is a key concept of GIS, most GIS users will nod their heads in agreement. But ask these same folks about how topology is handled in shapefiles and the nodding heads give way to shrugging shoulders. Why should GIS users care about topology? What are the advantages and disadvantages of storing polygon data in shapefiles rather than coverages? What Is Topology? In 1736, the mathematician Leonhard Euler published a paper that arguably started the branch of mathematics known as topology. The problem that led to Euler's work in this area, known as "The Seven Bridges of Königsberg," is described in the accompanying article "Conundrum Inspires Topology." More recently, the United States Census Bureau, while preparing for the 1970 census, pioneered the application of mathematical topology to maps to reduce the errors in tabulating massive amounts of census data. Today, topology in GIS is generally defined as the spatial relationships between adjacent or neighboring features. Mathematical topology assumes that geographic features occur on a two-dimensional plane. Through planar enforcement, spatial features can be represented through nodes (0-dimensional cells); edges, sometimes called arcs (one-dimensional cells); or polygons (two-dimensional cells). Because features can exist only on a plane, lines that cross are broken into separate lines that terminate at nodes representing intersections rather than simple vertices. In GIS, topology is implemented through data structure. An ArcInfo coverage is a familiar topological data structure. A coverage explicitly stores topological relationships among neighboring polygons in the Arc Attribute Table (AAT) by storing the adjacent polygon IDs in the LPoly and RPoly fields. Adjacent lines are connected through nodes, and this information is stored in the arc-node table. The ArcInfo commands, CLEAN and BUILD, enforce planar topology on data and update topology tables. Over the past two or three decades, the general consensus in the GIS community had been that topological data structures are advantageous because they provide an automated way to handle digitizing and editing errors and artifacts; reduce data storage for polygons because boundaries between adjacent polygons are stored only once; and enable advanced spatial analyses such as adjacency, connectivity, and containment. Another important consequence of planar enforcement is that a map that has topology contains space-filling, nonoverlapping polygons. Consequently, so-called cartographic (i.e., nontopological) data structures are no longer used by mainstream GIS software. Enter Shapefiles Shapefiles were introduced with the release of ArcView 2 in the early 1990s. A shapefile is a nontopological data structure that does not explicitly store topological relationships. Moreover, polygon features in shapefile format can contain one or more parts, so that disjunct and overlapping features can be represented. For example, an individual parcel that is split by a road can be represented alternatively as two separate polygons with two rings and two records in the attribute table or as one polygon with two parts and one record in the attribute table. A source of confusion for some users is that some ArcView GIS commands can result in spatially disjunct, multipart features. A primary advantage of shapefiles is that this simple file structure draws faster than a coverage does. This may be why the shapefile data structure was developed for ArcView GIS, a software program that was originally designed for data viewing rather than analysis. In addition, shapefiles can easily be copied and do not require importing or exporting as do .e00 format files. The shapefile specification is readily available, and a number of other software packages support it. These reasons have contributed to the emergence of the shapefile as a leading GIS data transfer standard. However, these advantages do not fully explain the resurgence of a nontopological data structure. Topological Digitizing and Editing One of the primary reasons topology was developed was to provide a rigorous, automated method to clean up data entry errors and verify data. The typical digitizing procedure is to digitize all lines, build topology, and label polygons and then clean up slivers, dangles, and under- and overshoots and build topology again, repeating the clean and build phases as many times as necessary.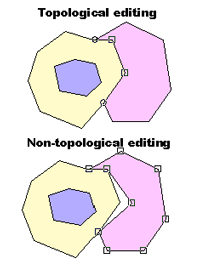 
What if the process did not start with the tangled mess of "cartographic spaghetti"? By approaching digitizing from a feature-centric perspective and enforcing planar topology when each feature boundary is digitized and labeled, sliver polygons, dangling nodes, missing labels, and multilabeled features would be eliminated. To be fair, computer hardware was not always powerful enough to support a feature-centric digitizing approach that requires on-the-fly calculation of geometric intersections (though a WYSIWYG digitizing approach was developed as far back as 1987!). Today's computers are powerful enough to support feature-centric digitizing for most GIS users. ArcView GIS supports such feature-centric digitizing through the Append Polygon, Split Polygon, and Split Line tools. With these tools users can add a polygon (or line) adjacent to an existing polygon and have boundaries match perfectly. ArcView GIS also supports topological editing of shared boundaries or nodes through the manipulation of vertices. File Sizes No Longer an Issue A second oft-cited advantage of topological data structures is smaller file sizes because shared vertices of adjacent polygons are not stored twice. Theoretically these files should be up to half the size of nontopological files. In practice however, shapefiles are rarely twice as large as the same data stored in coverages, in part because coverages require additional files to store the topological information. Attribute tables are often a large proportion of the overall file size but are the same size regardless of how feature geometry is stored. Moreover, although storage was often an important consideration in the past, the current low cost of storage means that for most GIS users storage space is not a constraint. Finding Adjacent Features Perhaps the most pervasive misunderstanding about shapefiles is that because topology is not explicitly stored, adjacent features cannot be found. However, adjacent features can easily be found by intersecting target polygons with other polygons in the same map and identifying the points of intersection of polygons that touch boundaries or overlap. The geometric intersections of adjacent features are calculated on the fly by comparing the vertices of adjacent features rather than looking up adjacent features in a table. For example, to find all the neighboring parcels of a parcel, select the parcel, choose Theme > Select by Theme from the View menu and choose "intersect" from the drop-down box and click on New Set to select all the parcels immediately adjacent to the originally selected parcel. More complex adjacency analyses can be accomplished by combining the selection by theme with a query for specific attributes such as identifying only the residential parcels adjacent to an industrial parcel. While some of the more complex adjacencies that involve direction (e.g., find the adjacent parcels to the east of a given road) are much more difficult to accomplish without stored topology, these analyses are not frequent nor are they a make-it-or-break-it requirement for typical users. Computing Adjacency Lists Although analytical operations that require adjacency information can be performed in ArcView GIS through the interface, performance requirements many necessitate building a table to store adjacency information. Two algorithms for building lists of adjacent features, described here, could be incorporated in an Avenue script. Although the representation of topological spatial relationships traditionally has been restricted to exactly adjacent neighbors, this restriction can be relaxed to find adjacent features. The notion of adjacency can be extended to include features that are within some distance (D) rather than exactly adjacent (D = 0). One advantage of computing adjacency lists is that adjacency can be defined in relation to the spatial precision of the coordinates, making analysis less sensitive to sliver polygons. These algorithms can find adjacency for polylines and polygons. If D > 0, adjacent points can also be identified. One algorithm creates an adjacency list using the so-called "brute-force" approach. In this simple algorithm, for every pair of features, it determines if these features intersect and stores the adjacent index values. The time required for this algorithm is proportional to the square of the number of features (N) or order O(N2). However, because adjacency is a reflexive spatial relation, the brute-force algorithm can be modified to store the index for reciprocal features as well. The time required for the modified algorithm is proportional to O(N(N-1)/2). A second algorithm uses a "divide and conquer" approach to recursively subdivide features into smaller and smaller groups. The reflexive brute-force approach is applied to these smaller groups. Because the number of features in each group is smaller than N, the overall number of intersection tests between two features is reduced considerably. Checking Topology in Shapefiles A planar-enforced shapefile can be created as described above or derived from a coverage. However, if nontopological editing methods are used, a shapefile can lose its planar topology during editing. Planar topology can be enforced on shapefiles with the assistance of some Avenue scripts. The logic of the algorithm is described here, and the scripts can be downloaded from ArcUser Online or the author's Web site. The first step in enforcing planar topology in a shapefile is to remove twisted or self-intersecting polygon rings and to ensure that the "inside" of the polygon is on the correct side of the polygon boundary. Next, gaps are identified by creating a rectangle that encompasses all the polygons of interest and serves as a backdrop. The polygons are subtracted from the rectangle containing all polygons. The remaining areas are gaps. A gap polygon is removed by merging it into an adjacent polygon or by making it a legitimate polygon. Overlaps are found by intersecting each polygon with all other polygons. If an intersection is found, then the polygon representing the overlap is created. Overlaps can be removed by deleting the overlapping area from one of the involved polygons. Once boundary changes have been made, the area and perimeter of each polygon should be recalculated. Conclusion The standard notion of topology in GIS centers around explicit representation of adjacent spatial relations and involves planar enforcement of geographic features. Although shapefiles do not explicitly store spatial relations, they can conform to planar enforcement. If, during map production or editing, planar enforcement is violated, then statistical summations that assume space-filling polygons could be inaccurate. Although this may be heresy to many users, there are advantages to using shapefiles that violate planar assumptions (i.e., shapefiles that have overlaps and/or gaps). Many useful analyses do not require data with precise planar topology, but these analyses are never conducted because it is assumed that base data must have topology. For instance, city and county governments find it extremely time-consuming and difficult to build parcel coverages because parcel boundary descriptions rarely match cleanly with adjacent parcels. Resolving boundary disputes is a very time-consuming process, often fraught with complicated legal issues. However, a standard query of parcel data performed with reasonably coincident boundaries (i.e., submeter accuracy) can be used to find landowners within a certain distance of a given location for notification purposes. Though the advantages previously attributed to topological data structures have become less clear, in large part because of improvements in computer performance, the bottom line is that GIS users need to adequately understand the data structures and use them appropriately. For more information, visit the author's Web site at www.ndis.nrel.colostate.edu/davet. About the author: David Theobald is a scientist at the Natural Resource Ecology Lab at Colorado State University and is the author of the book, GIS Concepts and ArcView Methods, which is available from the GIS Store. Further Reading Cooke, Donald F., and William H. Maxfield. "The Development of a Geographic Base File and Its Uses for Mapping," Proceedings of the Fifth Annual Conference of the Urban and Regional Information Systems Association, pp. 207-218, 1967. |
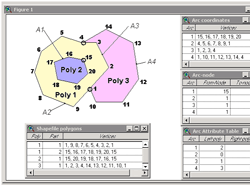However, unlike other simple graphic data structures, shapefile polygons are represented by one or more rings. A ring is a closed, non-self-intersecting loop. This structure can represent complex structures, such as polygons, that contain "islands." The vertices of a ring maintain a consistent, clockwise order so that the area to the right, as one "walks" along the ring boundary, is inside the polygon, and the area to the left is outside the polygon. 