By Aileen Buckley, Mapping Center Lead
You will often be prompted to select the geographic transformation when you are projecting data or setting the projection of a data frame in a map document. Here are some concepts that might help you understand what this is all about AND how to make the right selection.
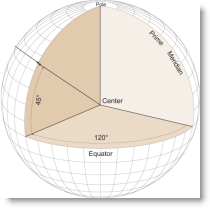
First, “geographic coordinates” are expressed in terms of latitude and longitude. “Latitude” is the north-south angular measure from the equator to the point of interest. “Longitude” is the east-west angular measure along the equator from the prime meridian to the point of interest’s longitude. Assuming that the earth is a sphere, geographic coordinates are determined relative to the center of the sphere – these coordinates are called “geocentric latitude and longitude”. (See the figure at the right; all figures are from Map Use: Reading and Analysis, 6th edition, Esri Press.)
Second, we know the earth is not a perfect sphere – it is elongated along the equator due to centrifugal force – its “equatorial radius” is longer than its “polar radius”. (The figure below is drawn using the real difference in length between the two axes which is not noticable at this scale.)
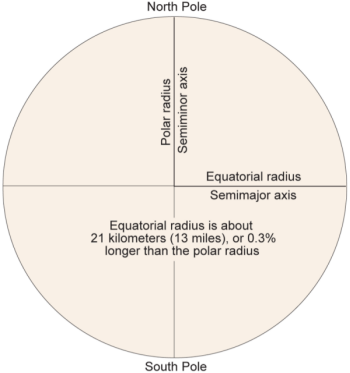
Therefore, instead of assuming that the earth is a sphere, we can more accurately assume it is an “oblate ellipsoid of revolution” (a sphere that is slighted squashed in at the poles), which we usually just call an “ellipsoid”. Rather than use coordinates defined by the spheroidal approximation of the earth, we use geographic coordinates expressed as latitude and longitude that are referenced to a particular ellipsoid of a defined shape and size. These coordinates are called “geodetic latitude and longitude”, and they will be slightly different from the geocentric ones. (See the figures below; in the one at the right, the difference between the equatorial and polar axes is greatly exaggerated!)

Different ellipsoids are used to approximate the earth, based on slightly different definitions of polar and equatorial axes of the ellipsoid – that is, the size and shape of the ellipsoid.
Third, imagine that the ellipsoid that is used as the model of the earth is then “positioned” relative to the surface of the earth to fit a specific area or use. This “fitted ellipsoid” becomes the frame of reference for specifying point coordinate locations, and it is called a “datum”. You should now be able to see how coordinates are datum dependent!
We have said that the ellipsoid is positioned to fit a specific area or use. If the ellipsoid is being used as the basis for a national or regional datum (i.e., frame of reference to define coordinates), it will be positioned to best fit the area of interest (like the North American Datum of 1927, or NAD27). If it is used as the basis for a world datum, the ellipsoid will most likely be positioned relative to the center of the earth’s mass (like the World Geodetic System of 1984, or WGS84).
Fourth, the datum, along with the prime meridian and angular units comprise a “geographic coordinate system” (GCS) which is referenced to the 3D ellipsoidal approximation to the earth. style=”text-decoration: underline” This is used to specify locations defined by latitude and longitude and heights above or below the ellipsoid at any latitude, longitude location.
Fifth, a “projected coordinate system” (PCS) results when the GCS is flattened down onto a 2D surface (e.g., paper, computer screen, etc.) A projected coordinate system is always defined relative to the GCS that it comes from, which in turn is based on a specified datum, which is defined in part by its ellipsoid.
SO – when you are asked to select the geographic transformation, you are being asked to choose which mathematical calculation will be used to convert coordinates referenced to one datum to coordinates referenced to another datum. This geographic or datum transformation is often embedded in the procedure to convert between coordinate systems, or in other words, the projection process. This process often involves more than one coordinate transformation. For example, let’s say you want to convert between two projected coordinate systems. This is what would happen in the projection process:
- Define the PCS that your data are currently in. The PCS includes the GCS.
- Unproject the data to geodetic latitude and longitude using the same GCS.
- Transform the data to geodetic latitude and longitude using the new GCS.
- Project the data to the new PCS using the new GCS.
You can see that when you select the PCS you want to use, you also need to select the geographic transformation (step 3 above) because there are multiple mathematical calculations that can be used to define how the coordinates will be converted to the new GCS. Note that even if you are converting from one GCS to another GCS, you still need to define the geographic transformation; however, the will be no need to convert from PCS to GCS and visa versa during this kind of projection process.
So how do you choose the geographic transformation that should be used? Here are two Esri Knowledge Base articles that can help you:
HowTo: Select the correct geographic (datum) transformation when projecting between datums. This article contains links to downloadable zip files (for different versions of the software) that contain a list of all available datum transformations and their appropriate geographic areas of use.
HowTo: Determine which NAD_1983_To_WGS_1984 transformation to use. The gist of this article is summarized below:
- NAD_1983_To_WGS_1984_1 – for the entire North American continent.
- NAD_1983_To_WGS_1984_2 – for the Aleutian islands.
- NAD_1983_To_WGS_1984_3 – for Hawai’i.
- NAD_1983_To_WGS_1984_4 – superseded by _5; this transformation method should no longer be used!
- NAD_1983_To_WGS_1984_5 – for the 48 contiguous United States.
- NAD_1983_To_WGS_1984_6 – for the Canadian province of Quebec.
- NAD_1983_To_WGS_1984_7 – for the Canadian province of Saskatchewan.
- NAD_1983_To_WGS_1984_8 – for the Canadian province of Alberta.
Note that geographic transformations work in either direction. For example, the transformation listed as NAD_1983_To_WGS_1984_5 transforms from NAD 1983 to WGS 1984, as well as from WGS 1984 to NAD 1983. When using the Project Tool, the geographic transformation is recorded in the metadata.
To learn more about geographic transformation methods, check out:
- ArcGIS online help at: http://webhelp.esri.com/arcgisdesktop/9.3/index.cfm?TopicName=Geographic_transformation_methods
- Map Use: Reading and Analysis, 6th edition, by Kimerling, Buckley, Muehrcke and Muehrcke. Esri Press. See Chapter 1: The Earth and Earth Coordinates.
- The Encyclopedia of Geographic Information Science, edited by Karen Kemp. Sage Publications. See the entries for “Datum”, “Transformations, Coordinate” and “Transformations, Datum”.
Thanks to Melita Kennedy, David Burrows, and Rob Juergens of the ArcGIS Projection Engine Team for helping me to make sure I said things correctly!


Article Discussion: