ArcUser Online

Incorporating Expert Knowledge
New fuzzy logic tools in ArcGIS 10
By Gary L. Raines, Don L. Sawatzky, and Graeme F. Bonham-Carter

This article as a PDF .

For many spatial modeling problems, experts can describe the decision-making process used to predict real-world phenomena: the favorability for locating mineral deposits or archaeological sites, the occurrence of hazards such as landslides or disease outbreaks, the habitat of specific animals or plants, or the optimal site for a business. For most interesting spatial problems, expert knowledge is often expressed in terms such as nearness to some feature or by statements involving sometimes or maybe. Such semantic descriptions are useful but imprecise.

Figure 1: Graphic example of the membership function Tallness. The semantic statement might be, "a height of 82 inches is always considered tall," whereas "a height below 38 inches is never considered tall." A height of about 70 inches is ambiguous for tallness and given a membership value of 0.5.5.

Fuzzy logic is used extensively in poorly definable engineering applications such as the anti-lock braking system (ABS) that controls brakes in cars; the focusing and exposure controls on digital cameras; and the control of water intake, temperature, and other settings in high-end washing machines. Fuzzy logic provides an approach that allows expert semantic descriptions to be converted into a numerical spatial model to predict the location of something of interest.

In addition to Boolean logic and Weighted Overlay tools in ArcGIS 10, two new Overlay tools—Fuzzy Membership and Fuzzy Overlay—are available. Overlays using fuzzy logic provide more flexible weighting of evidence and combinations of evidence than traditional Boolean or Weighted Overlays. These new tools in ArcGIS are derived from the Spatial Data Modeller (SDM) toolbox developed by the U.S. Geological Survey and the Geological Survey of Canada. [SDM is a collection of geoprocessing tools for spatial data modeling that is available from ArcScripts at http://arcscripts.esri.com/details.asp?dbid=15341.] The Fuzzy Logic tool is just one of many methods available from the SDM toolbox that includes weights of evidence, logistic regression, expert systems, and model validation.

A Nonspatial Example

Figure 2: Diagram of the Categorical Weights tool available in the Spatial Data Modeller toolbox

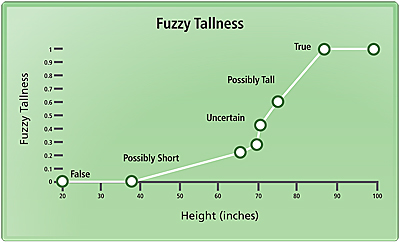
Table 1 illustrates a simple example of a nonspatial Boolean and fuzzy logic model through a chart on tallness. Boolean logic deals with situations that can be true or false. Fuzzy logic allows degrees of truth (expressed as a membership function) in the range of zero to one. In this example, an expert uses fuzzy membership values to define the importance of two characteristics of people (tallness and oldness) to be used as predictive evidence (values between 0 and 1). The expert also defines how the evidence is combined, in this example using fuzzy AND and OR operators.

Probability is a special case of fuzzy membership. If the probability of truth is 0.8, then the probability of false is 0.2 (i.e., if the probability of an event occurring is x, then the probability of the event not occurring is always 1-x). This additive-inverse property of probability statements is not required in fuzzy logic. Fuzzy membership can be thought of as the "possibility" that the statement is true.

In a Boolean model, the height of Marge (listed in Table 1) is absolutely not tall or tallness is zero, whereas in a fuzzy logic model, Marge's height is somewhat short with a tallness of 0.42. Generally, a membership of 0.5 indicates an ambiguous situation that is neither true nor false. An example of a membership function with semantic descriptors (e.g., possibly short, possibly tall) is shown graphically in Figure 1. Fuzzy membership thus provides sensitivity to the subtle aspects of the process being modeled. In addition, a variety of fuzzy combination operators are available that greatly extend the simple AND and OR operators used in Boolean logic and allow the flexibility and complexity incorporated in making many real-world decisions to be modeled.

Evidence

Nonspatial Models

Table 1: A nonspatial example comparing Boolean logic with fuzzy logic. In Boolean logic, truth is "crisp," zero or one. In fuzzy logic, truth has degrees between zero and one. Fuzzy tallness and fuzzy oldness are the membership in the concepts tallness and oldness. Boolean tallness and Boolean oldness are binary memberships in these concepts. Thus in Boolean logic, a person is either tall or not; whereas in fuzzy logic, a person can be somewhat tall. The operators AND and OR are used for combining evidence in both methods.

A Spatial Example

In a fuzzy logic model in ArcGIS, evidence rasters are assigned membership values with the Fuzzy Membership tool. Table 2 defines the fuzzy membership functions available. Memberships are combined using the Fuzzy Overlay tool to select a fuzzy combination operator based on how the evidence interacts.

Table 3 defines five fuzzy operators. In a given model, different operators may be used. These operators provide greater flexibility than a weighted-sum or weighted-overlay model and let the expert incorporate greater sensitivity based on knowledge of how the evidence interacts. In practice, operators for combining evidence are relatively easy to select, but fuzzy membership may require some tuning of the membership parameters to represent expert knowledge.

A Simple Expert Semantic Summary

Figure 3: A demonstration of a simple fuzzy logic model. Categorical membership is described in Figure 2. The other tools are Overlay tools in ArcGIS 10.

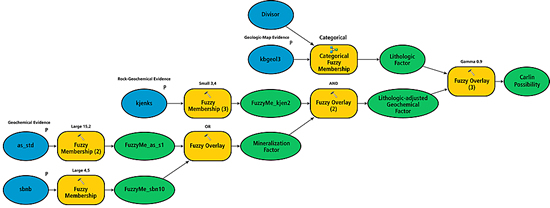
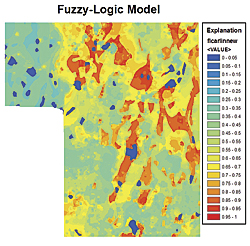
Figure 3 is a simple example of a fuzzy logic spatial model. This geologic model for Carlin-type gold deposits uses datasets that are available with the Spatial Data Modeller tools (www.ige.unicamp.br/sdm/default_e.htm). [Carlin-type gold deposits, with ore grades commonly between 1 and 5 grams per ton, are primarily mined from open pits in Nevada. They are named for the most prolific goldfield in the Northern Hemisphere, the Carlin Trend Field.] From a semantic description of the criteria for finding Carlin-type gold deposits, a simplified expert semantic model might consist of the following statements:

• High values of antimony (Sb) or arsenic (As) are favorable for Carlin-type gold. Use stream-sediment geochemistry to define a mineralization geochemical factor.
• Host rocks of Carlin-type deposits are primarily Paleozoic and Mesozoic dirty carbonate rocks. Use a geologic map to define a lithologic factor.
• Dirty carbonate rocks are chemically low in potassium (K). Use stream-sediment geochemistry to make a lithologic adjustment to the mineralization geochemical factor. Elevated K differentiates Carlin-type gold deposits from volcanic-rock-hosted gold deposits, although both types are high in Sb or As.

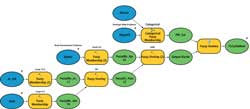
From these semantic statements, a simple outline of the fuzzy logic model can be defined.

A Simple Fuzzy Logic Model

Frequently such models have submodels or factors that describe complex aspects of the spatial model. These submodels often represent factors defined by a single discipline; thus, "the Expert" for the entire model is—in practice—often a team of experts who bring knowledge from diverse fields when defining the decision process. A final model is derived by combining the factors. The following semantic statements describe the process for determining the geochemical, lithologic-adjusted geochemical, and lithologic factors in the model shown in Figure 3.

Boolean and fuzzy logic models. The model uses Bitwise OR and AND in place of Fuzzy OR and AND. The fuzzy gamma is replaced by a Bitwise OR, which is most similar to a fuzzy gamma.

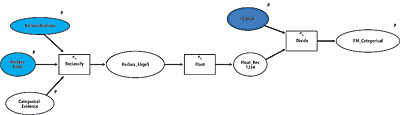
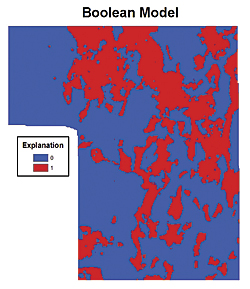
Mineralization Geochemical Factor

Use the Large Fuzzy Membership tool for assigning fuzzy membership values to Sb and As. Tune the parameters for the Large Fuzzy Membership tool to produce fuzzy evidence maps acceptable to the expert.

Combine the Sb and As fuzzy maps with a Fuzzy OR operator. Use the Fuzzy Membership tool for K, again tuning the parameters for the Small Fuzzy Membership tool to make an acceptable map.

Lithologic-Adjusted Geochemical Factor

Use the Fuzzy AND operator to combine the mineralization geochemical factor with the K membership.

Lithologic Factor

Assign the fuzzy memberships to the various lithologies present on the geologic map following guidance from the expert and using the Categorical Fuzzy Membership tool in the Spatial Data Modeller toolbox and diagrammed in Figure 2.

Combine the lithologic-adjusted geochemical factor with the lithologic factor using the Gamma combination operator to produce the Carlin-type gold possibility map. Tune the gamma parameter value to produce an acceptable combination.

Once the model shown in Figure 3 is assembled, it will be necessary to adjust the fuzzy membership parameters to tune fuzzy memberships to represent properly the expert's concepts. This tuning can be done graphically in a spreadsheet or, more often, spatially by inspecting rasters. Using iteration methods in separate tuning models is useful for quickly computing a selection of rasters with a range of parameters. Experts will recognize the best representation of the spatial data. When disagreements occur about the optimal tuning of the fuzzy memberships, multiple models can be built quickly representing different opinions and tested during model validation. Figure 4 provides a comparison of the Boolean and fuzzy logic models. A weighted sum model would be more similar to—but not the same as—the fuzzy logic model.

Figure 4: The simple fuzzy logic model for Carlin-type gold deposits

After completing the model or models, it is important to validate the results. If there are known examples of what is being modeled (i.e., known deposits, animal sightings), these can be used to test how well the model classifies known examples. The Area Frequency tool in the Spatial Data Modeller toolbox provides a measurement of the efficiency of prediction measure. Lacking known examples, the judgment of the experts and field testing are required to validate the model. For more information, contact Gary Raines at garyraines.earthlink.net.

Further Reading

An, P., W. M. Moon, and A. N. Rencz, 1991. "Application of fuzzy set theory for integration of geological, geophysical and remote sensing data." Canadian Journal of Exploration Geophysics, V. 27, No. 1, pp. 1�11.

Bonham-Carter, G. F., 1994. Geographic Information Systems for Geoscientists—Modelling with GIS. New York: Elsevier Science, pp. 291�302.

Eddy, B. G., G. F. Bonham-Carter, and C. W. Jefferson, 2010. "Mineral potential analyzed and mapped at multiple scales—a modified fuzzy logic method using digital geology," Harris, J. R. (editor), in GIS Applications in Earth Sciences: Special Publication. Geological Association of Canada, Special Publication 44, pp. 143�162.

Nykanen, V., D. I. Groves, V. J. Ojala, P. Eilu, and S. J. Gardoll, 2008. "Reconnaissance-scale conceptual fuzzy-logic prospectivity modeling of iron oxide copper-gold deposits in the northern Fennoscandian Shield," Australian Journal of Earth Science. V. 55, pp. 25�38.

Raines, G. L., and G. F. Bonham-Carter. 2006. "Exploratory Spatial Modelling Demonstration for Carlin-type deposits, Central Nevada, USA, using Arc-SDM," Harris, J. R. (editor), in GIS Applications in Earth Sciences: Special Publication. Geological Association of Canada, Special Publication 44, pp. 23�52.

About the Authors

Gary L. Raines retired as a research geologist for the U.S. Geological Survey in Reno, Nevada. His research focused on the integration of geoscience information for predictive modeling in mineral resource and environmental applications. He now teaches classes in spatial modeling.

Don L. Sawatzky retired as a research geologist for the U.S. Geological Survey in Reno, Nevada. His research focused on computerized analyses in remote sensing, geophysics, and structural geology.

Graeme F. Bonham-Carter retired as a research geologist for the Geological Survey of Canada, Ottawa. He is interested in applications of GIS to mineral exploration and environmental problems. For 10 years, he was editor-in-chief of Computers & Geosciences, a journal devoted to all aspects of computing in the geosciences.