It is common to see data in a geographic coordinate system (GCS). It’s an easily understood, world-wide coordinate system, and many datasets use GCS as part of their spatial reference. However, there are drawbacks to using a geographic coordinate system. One of the most prominent is evident when doing surface analyses over terrain with X,Y coordinates stored in latitude longitude and with elevation values stored in linear units such as meters. This is a problem because degrees of latitude and longitude are angular units measured on a sphere, and meters are linear units measured along a plane. Degrees of longitude are also of variable length, depending upon the latitude, and degrees of longitude represent significantly larger distances than meters over most of the globe (except very close to the poles).
For analyses is best to project your data into a projected coordinate system (PCS) so all measurements (X, Y, and Z) are in the same unit of measure. Sometimes, for visualization purposes when no further analysis is necessary, we can use a simple workaround to the problem of mismatched units. That is, we can apply a Z-factor to scale the Z units to approximately the same size.
Here’s an example. We’ll create a hillshade of a DTED tile of Hawaii to illustrate what happens when the elevation dataset is in a GCS (GCS_WGS_1984 in this case) with elevation units in meters.
Executing: HillShade n19 “C:WorkSpaceBlog TopicsDetermining Z-factor for surface rastersBlogData.gdbHillSha_n193″ 315 45 NO_SHADOWS 1Start Time: Thu Dec 09 12:38:34 2010WARNING 000869: Z factor: The Z units of the output geographical spatial reference are undefined. A default Z factor of 1 was used.Succeeded at Thu Dec 09 12:38:37 2010 (Elapsed Time: 3.00 seconds)
Note that the Hillshade tool completed, but flagged the process with a warning.
The resulting layer looks like this: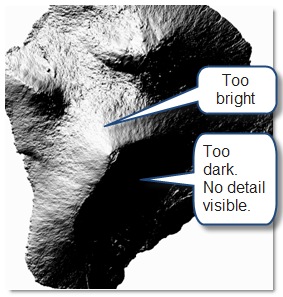
This hillshade has too much contrast; the shadowed areas appear black, and the sunny areas are almost white. This is because the slopes calculated by the hillshade algorithm were unrealistically steep, due to mismatched XY and Z units. To account for the difference in units we can “scale” the elevation meters into something closer to the decimal degrees.
The calculation we’ll use is:
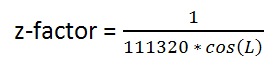
where:
• “L” is the mid-latitude of the dataset
• 111320 is the number of meters in one degree, in radians, at the equator (approximated using GCS_WGS_1984).
Manually it would look like this:
For L = 19.500 degrees ? 0.340 radians
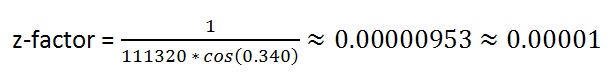
We’ll round the result up to 0.00001. Now we will re-run the Hillshade tool and apply the z-factor.
Executing: HillShade n19 “C:WorkSpaceBlog TopicsDetermining Z-factor for surface rastersBlogData.gdbHillSha_n191″ 315 45 NO_SHADOWS 0.00001Start Time: Thu Dec 09 12:42:11 2010Succeeded at Thu Dec 09 12:42:13 2010 (Elapsed Time: 2.00 seconds)
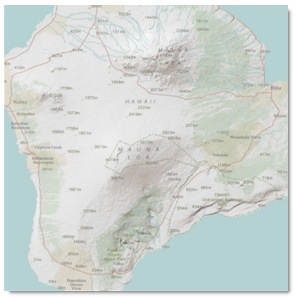
The new hillshade looks like this:

This is the expected result. We can apply a transparency, and place it over a scanned map or other colored layer to suggest the relief of the terrain.
The z-factor calculation isn’t difficult, but is a pain to do over and over, which makes this a great opportunity to implement it as a script tool. Here is a code sample for an ArcGIS 10 geoprocessing script tool that would perform the calculation. The input could be a Dataset, Raster Dataset, or Raster Layer and the output would be a double (numeric with decimal places).
import os, sys, math, decimal, traceback
import arcpy
# INPUT DATASET, Required
dataset = arcpy.GetParameterAsText(0)
try:
#get the top and bottom
desc = arcpy.Describe(dataset)
extent = desc.Extent
extent_split = [extent.XMin,extent.XMin,extent.XMax,extent.XMax]
top = float(extent_split[3])
bottom = float(extent_split[1])
#find the mid-latitude of the dataset
if (top > bottom):
height = (top – bottom)
mid = (height/2) + bottom
elif (top < bottom): # Unlikely, but just in case
height = bottom – top
mid = (height/2) + top
else: # top == bottom # Again, unlikely but just in case
mid = top
# convert degrees to radians
mid = math.radians(mid)
# Find length of degree at equator based on spheroid’s semi-major axis
spatial_reference = desc.SpatialReference
semi_major_axis = spatial_reference.semiMajorAxis # in meters
equatorial_length_of_degree = ((2.0 * math.pi * float(semi_major_axis))/360.0)
# function:
# Z-Factor = 1.0/(111320 * cos(mid-latitude in radians))
decimal.getcontext().prec = 28
decimal.getcontext().rounding = decimal.ROUND_UP
a = decimal.Decimal(“1.0″)
#b = decimal.Decimal(“111320.0″) # number of meters in one degree at equator (approximate using WGS84)
b = decimal.Decimal(str(equatorial_length_of_degree))
c = decimal.Decimal(str(math.cos(mid)))
zfactor = a/(b * c)
zfactor = “%06f” % (zfactor.__abs__())
arcpy.SetParameterAsText(1,str(zfactor))
# return Z factor message
arcpy.AddMessage(r”Z-factor: ” + (str(zfactor)))
except:
print “General Error:”
tb = sys.exc_info()[2]
tbinfo = traceback.format_tb(tb)[0]
pymsg = tbinfo + “n” + str(sys.exc_type)+ “: ” + str(sys.exc_value)
arcpy.AddError(pymsg)
print pymsg
You could copy this code into a text editor and save it with a “.py” extension, then add it as a script tool.
Of course, we should make sure that the input dataset/layer is in a GCS and that the extent of the dataset is something reasonable (within -180 to 180 and 90 to -90). To do this we would use a tool validator that checks before we run it. The following tool validator snippet for updateMessages will do just that and throw an error if the dataset/layer doesn’t meet our criteria.
def updateMessages(self):
“””Modify the messages created by internal validation for each tool
parameter. This method is called after internal validation.”””
# check input is geographic
if (self.params[0].altered == True):
spatial_ref = arcpy.Describe(self.params[0].value).SpatialReference
if (spatial_ref.Type != “Geographic”):
self.params[0].setErrorMessage(“%s is not in a Geographic Coordinate System.” % self.params[0].Value)
# check that the extent is valid
desc = arcpy.Describe(self.params[0].value)
extent = desc.Extent
extent_split = [extent.XMin,extent.YMin,extent.XMax,extent.YMax]
bExtOK = True
for splst in extent_split:
if (splst == ’1.#QNAN’):
bExtOK = False
if (bExtOK == False):
self.params[0].setErrorMessage(“%s does not have a valid extent.” % self.params[0].Value)
return
Content provided by Matt Funk
Commenting is not enabled for this article.