This is the second of a four-blog series discussing Distance Analysis. In the first blog, we demystified distance analysis. In it, we identified the three major aspects when performing distance analysis, 1) calculate the straight-line distance adjusting for the encountered features in the landscape, 2) determine the rate the adjusted straight-line distance is experienced by the traveler to create a distance accumulation raster, and 3) connect identified locations with optimal paths over the accumulation raster.
This blog will focus on the first component, calculating the adjusted straight-line distance. There are several adjustments that can be made when measuring distance. We will explore how to determine the straight-line distance between locations and adjust that distance with barriers and the surface distance.
Yes, straight-line distance, barriers, and surface distance can work together to determine distance. Our goal when calculating the adjusted straight-line distance is to accurately determine the shortest physical distance a traveler must travel between locations. The shortest physical distance for a traveler is related to the mode of travel. There is always an implicit or explicit mode of travel when calculating the distance between locations.
When calculating the basic straight-line distance, the implicit mode of travel of the traveler is flying above the surface. However, if the traveler is on foot, certain features in the landscape may be in the way which forces the traveler to move around them. The shortest physical distance is a function of the mode of travel and is not related to the traveler themselves. That is, an ant and an elephant, when moving between locations and there is something in their way, will travel the same shortest physical distance. They may do so at different rates, but that is the topic of the next blog. However, the shortest physical distance for a bird flying between the same two locations will probably be less if there is nothing in its way.
Let’s get started and first examine the most basic distance calculation, straight-line distance or Euclidean distance. This is the distance calculation that most people think of when determining the distance between locations. It is the distance you would measure with a ruler on a paper map. It is generally referred to as the distance a crow or airplane would fly between the two points. The straight-line distance ignores the surface or landscape between the locations.

If you are not a bird or an airplane and do not care about the landscape between the locations, straight-line distance is a good approximation. See Calculating Straight line distance for additional information.
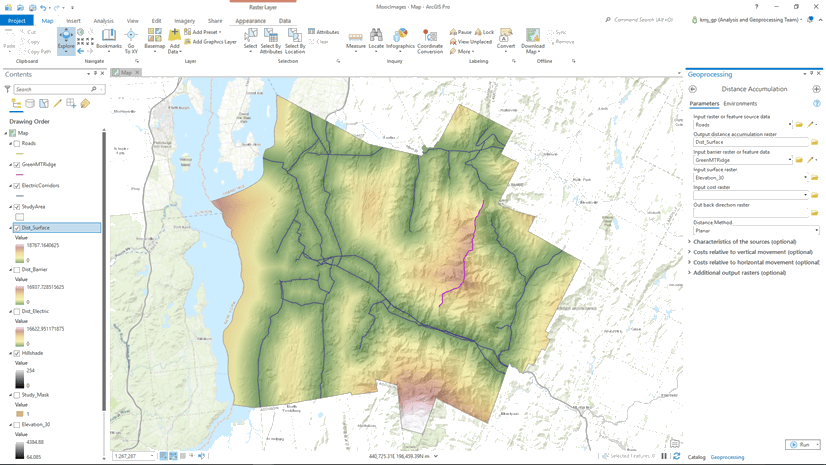
The Distance Accumulation tool is used to determine how far each cell location is from an identified source. A source can be an airport, a ranger station, or a road. If there are multiple sources, then for each cell location, the distance to the closest source is calculated.
Generally, there are three measures that define the spatial relationship of the locations you are determining the distance between,
- how far it is between the locations
- what direction is one location to the other
- how would you travel to get between the locations
The Distance Accumulation tool allows you to create each of these as output. While the Distance Allocation tool allows you to identify which is the closest source.
As mentioned, the straight-line distance assumes the mode of travel is flying above the surface. But what if you are walking on the surface and there is something between the locations? That is, a barrier exists.
What comes to mind when you think of a barrier? A cliff? A river? A major road?
These can be barriers, but, once again, it depends on the traveler and their mode of travel. In certain cases, these features are hard barriers and to move around them you would need to find a bridge or an overpass in the cases of the river or road.
A barrier impedes the movement between two locations. For a hiker, a lake might be a barrier and you need to detour around it. The resulting effect is the physical distance that you must travel between the locations is greater.
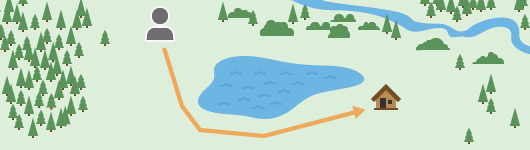
What if there is a boat at the water’s edge? Is the lake still a barrier? It is for the ant and the elephant, but maybe not for you as a human.
A barrier effects the three output distance measures in the following ways:
- the distance between locations can be greater
- the straight-line direction to the source remains the same whether the barrier exists or not if the barrier does not change which the closest source is for the location
- the direction of travel will change when a barrier is in the way.
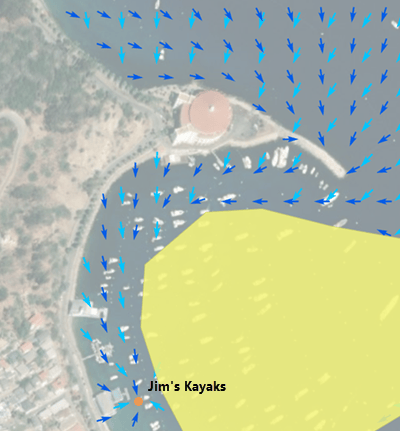
Let’s look a little deeper into barriers. As alluded to, a barrier is relative to the traveler. If I am in a kayak or I am a sea mammal, the land becomes a barrier to my water movement.
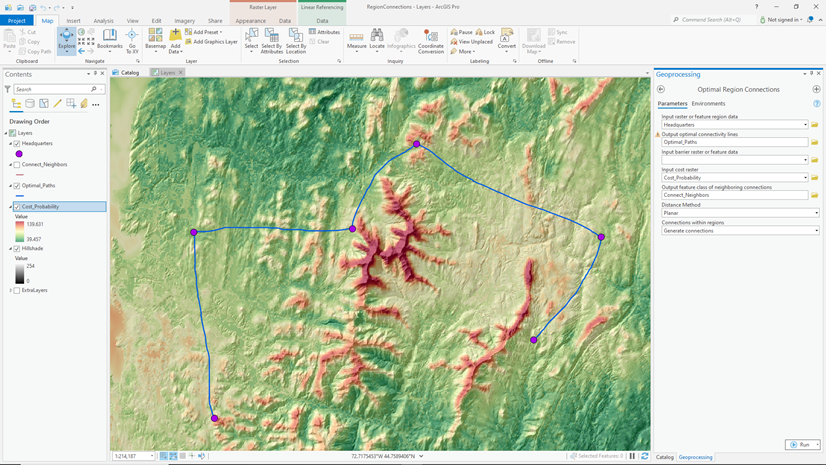
In the image below, for a sampling of locations, the light blue arrow indicates the straight-line direction back to the Jim’s Kayaks rental, while the dark blue arrows indicate the direction to paddle from the location to return to the rental.
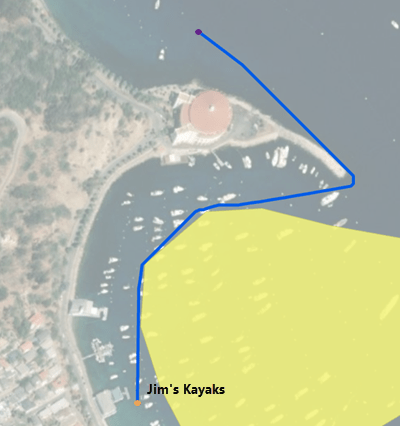
If you are in the northern part of the study area at the location identified by the red point, the shortest path to paddle to return to Jim’s Kayaks is indicated by the blue line below. You must paddle around the peninsula.
A barrier for a migratory bird or an airplane might be a storm or a smoke plume from an active volcano. A barrier for a small mammal might be rock or a stream. For a turtle, it might be a log. In all these cases, the traveler needs to move around the barrier, the physical distance increases, and the travel direction alters.
Certain features may be a hard barrier which you cannot pass through. Other features may be just difficult or costly to move through and are not really barriers. In the latter case, these features affect the rate the distance values are encountered and should possibly be modeled in a cost surface. It may turn out the traveler may move around these features when traveling the optimal path between the locations, but it is because the features are too costly to move through, not that they are barriers.
See Incorporating barriers for additional information.
A second adjustment to the physical distance that must be traveled when moving over the landscape is the actual distance that you would need to travel accounting for going up and down the undulations in the surface. That is, if traveling over the landscape, you need to travel the hypotenuse when going over the uphills and downhills.
Another way to visualize this. If you have an exercise wrist band, you would register more steps going over a hill than if it were flat. These added steps increase the physical distance that must be traveled and is referred to as the surface distance.
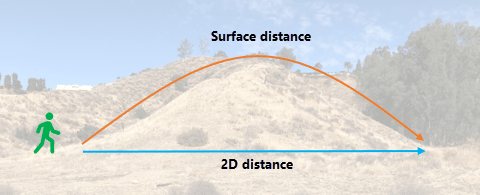
Generally, an elevation raster is input as the surface raster. See The surface distance for additional information.
To accurately determine the shortest physical distance that must be traveled between locations the mode of travel of the traveler is identified. When on foot, the straight-line distance (as the crow flies) may be adjusted with barriers and the surface distance. At this point we now have the most accurate measure of the shortest physical distance a traveler should travel between locations.
In the next blog we will discuss how to determine the rate the traveler will encounter this distance. That is, we will simulate a traveler moving on the landscape. We will account for the different land use types, the effort to overcome slopes, and the effort if heading into a wind or current. Determining the rate, the adjusted straight-line distance is experienced is referred to as the cost distance.
The final blog in this series will discuss the different methods to connect locations with optimal paths.
In this blog we focused on determining the shortest physical distance that must be traveled between locations. The physical distance is a function of the mode of travel of the implicit or explicit traveler. Even though there are several variations when calculating the shortest physical distance, it is just distance. And, that distance is relative.

Article Discussion: